Optimization of suspension support structure of cardiac pump and analysis of anti-hemolysis function
-
摘要:目的
优化心脏泵的支承结构,以期增加悬浮力和减少溶血。
方法设计新型离心式心脏泵的悬浮支承结构,在导流锥附近设计扇形开孔,在悬浮轴承底部设计辅助叶片,并通过计算流体动力学方法比较改进结构前后心脏泵的悬浮力和抗溶血性能。
结果改进后心脏泵出入口压差值随流量增大而减小,且随叶轮转速提高而增大,与心脏泵在流体中流量压差情况相同,心脏泵的压差值在允许范围内。叶轮内血液最大速度低于溶血易发生速度(6 m/s),结构改进具有可行性。改进后,叶轮上下表面的压差随着流量的增大而减小,轴向方向向上的悬浮力增大,叶轮受到的悬浮力增加,悬浮性能得到改善;在液力轴承悬浮间隙处,流体平均流速提升,心脏泵底部区域的剪切应力最大值与高剪切应力区域占比均相对降低;液力轴承悬浮间隙处和底部区域溶血减少,改进结构后的心脏泵溶血指数相较于改进前降低了12%。
结论优化后的心脏泵悬浮性能得到改善,且溶血指数降低。改进的悬浮结构也可应用于其他离心式心脏泵,其在增加心脏泵悬浮力与减少悬浮轴承间隙处溶血方面具有实际价值。
Abstract:ObjectiveTo optimize the supporting structure of the heart to increase the suspension force and reduce hemolysis.
MethodsThe suspension support structure of a new centrifugal heart pump was designed, the fan-shaped opening was designed near the diversion cone and the auxiliary blade was designed at the bottom of the suspension bearing. The suspension force and hemolysis performance of the heartpump before and after optimization were compared by using the computational fluid dynamics method.
ResultsAfter improvement, the inlet and outlet pressure difference of the heart pump decreased with the increase of the flow rate, and increased with the increase of the impeller speed. It was the same as the flow pressure difference of the heart pump in the fluid, and the pressure difference of the heart pump was within the allowable range. The maximum blood velocity in the impeller was less than the rate of hemolysis (6 m/s). Structural improvement was feasible. The pressure difference between the upper and lower surfaces of the impeller decreased with the increase of flow rate, and the axial upward suspension force increased, the suspension force of the impeller increased, and the suspension performance was improved. At the suspension gap of the hydraulic bearing, the average fluid velocity increased, the maximum shear stress and the proportion of high shear stress in the bottom region of the heart pump were relatively reduced, and the hemolysis indexes at the suspension gap and the bottom region of the hydraulic bearing was decreased, and the hemolysis indexes of the heart pump was reduced by 12% after the improved structure compared with that before the improvement.
ConclusionThe suspension performance of the optimized heart pump is improved and the hemolysis indexes are reduced. The improved suspension structure can also be applied to other centrifugal heart pumps, which has practical value in increasing the suspension force of the heart pump and reducing hemolysis in the suspension bearing clearance.
-
Keywords:
- centrifugal heart pump /
- suspension bearing /
- suspend gap /
- hemolysis indexes /
- suspension force
-
近年来,心血管疾病的发生率呈逐年上升趋势,且心血管疾病死亡居中国城乡居民总死亡原因的首位[1]。心脏移植是相对有效的心血管疾病治疗方式,但存在匹配难度大、心脏供体少等问题[2]。目前,临床医师大多采用人工心脏泵替代受损心脏的方案治疗心血管疾病患者,经多年研究,人工心脏泵技术已从第1代仿真心脏泵发展为第2代轴流式心脏泵和目前使用较多的第3代悬浮式心脏泵[3-4]。近年来,众多国内外研究人员从叶轮与泵壳在流场中的关系等方面入手,探讨不同心脏泵与壳体之间尺寸对人工心脏泵抗溶血性能的影响,但关于悬浮支承结构与液力轴承悬浮间隙处的研究则较少见。本研究设计了一种新型离心式心脏泵的悬浮支承结构,以期增加悬浮力和减少溶血,现报告如下。
1. 资料与方法
1.1 心脏泵三维模型及网格划分
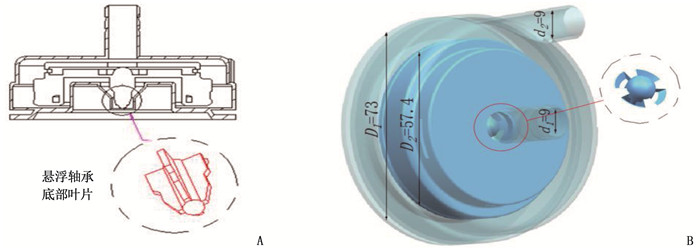
本研究对已有的离心式心脏泵结构进行研究后,设计出一种新型悬浮支承结构的离心式人工心脏泵。对心脏泵结构进行三维建模,提取和切分泵内流场区域,新型结构的悬浮轴承底部设计了4个小叶片,通过叶轮旋转带动底部小叶片转动,见图 1。心脏泵中,叶轮的入口直径d1为9 mm, 出口直径d2为9 mm; 于导流锥附近设计扇形开孔,使血液能够流入叶轮底部; 叶片结构采用直叶片,叶片出口宽度为3 mm, 厚度为3 mm。与传统泵壳相比,新型结构泵壳从结构方面进行了改进,即考虑到叶轮底部增加辅助叶片的设计,在泵壳底部设计了V型槽。设计底部轴承与开孔的目的是使叶轮上下表面形成压力差,减小心脏泵所需的悬浮力,更好地促进底部间隙处血液流动,进而减小血液滞留区,提升抗溶血性能。
对各部分流域表面进行网格划分,为了促进充分发展流动,将模型划分为入口、蜗壳、叶轮、出口4个部分。本研究的物理模型流体入口及出口较为规则,且入口段包含流体湍流发展段,因此进行混合网格划分,并采用高质量的结构化网格强化模型出入口的计算。鉴于贴壁处流体动量交换及质点脉动的剧烈性,严格计算各流动区域壁面首层网格高度,以确保底层网格处黏滞力计算准确。在结构网格与非结构网格交界处进行过渡加密,确保网格形式变动时各离散点上的值不发生突变; 对于非结构网格部分,在贴壁处及叶轮处设置3~5层边界层,保证后续动网格计算的准确性,同时起到优化计算收敛的效果。模型的网格划分单元数为397万,最小网格质量为0.35, 见图 2(出口部分网格见右侧小图,并进行网格无关性验证)。
1.2 控制方程与计算方法
心脏泵内的血液流动服从流体动力学的基本方程,基于单相牛顿流体模型,连续性方程如下:
$$ \frac{\partial \rho}{\partial t}+\nabla \cdot(\rho V)=0 $$ (1) 式中, ρ表示流体的密度, V表示速度向量。沿不同方向的动量方程如下:
$$ \frac{\partial(\rho \mu)}{\partial t}+\nabla \cdot(\rho \mu V)=-\frac{\partial \rho}{\partial x}+\frac{\partial \tau_{x x}}{\partial x}+\frac{\partial \tau_{y x}}{\partial y}+\frac{\partial \tau_{z x}}{\partial z} $$ (2-1) $$ \frac{\partial(\rho \nu)}{\partial t}+\nabla \cdot(\rho \nu V)=\frac{\partial \rho}{\partial y}+\frac{\partial \tau_{x y}}{\partial x}+\frac{\partial \tau_{y y}}{\partial y}+\frac{\partial \tau_{zy}}{\partial z} $$ (2-2) $$ \frac{\partial(\rho w)}{\partial t}+\nabla \cdot(\rho w V)=-\frac{\partial p}{\partial z}+\frac{\partial \tau_{x z}}{\partial x}+\frac{\partial \tau_{y z}}{\partial y}+\frac{\partial \tau_{z z}}{\partial z}+\rho g $$ (2-3) 式中, μ、ν、w表示速度分量, g表示重力加速度。应力张量τ为对称张量,分量形式如下:
$$ \tau_{x x}=-\frac{2}{3} \mu(\nabla \cdot V)+2 \mu \frac{\partial \mu}{\partial x} $$ (3-1) $$ \tau_{y y}=-\frac{2}{3} \mu(\nabla \cdot V)+2 \mu \frac{\partial \nu}{\partial y} $$ (3-2) $$ \tau_{z z}=-\frac{2}{3} \mu(\nabla \cdot V)+2 \mu \frac{\partial w}{\partial z} $$ (3-3) $$ \tau_{x y}=\tau_{x y}=\mu\left(\frac{\partial \nu}{\partial x}+\frac{\partial \mu}{\partial y}\right) $$ (3-4) $$ \tau_{x z}=\tau_{z x}=\mu\left(\frac{\partial \mu}{\partial z}+\frac{\partial w}{\partial x}\right) $$ (3-5) $$ \tau_{y z}=\tau_{z y}=\mu\left(\frac{\partial w}{\partial y}+\frac{\partial \nu}{\partial z}\right) $$ (3-6) 式中, μ表示血液的动力黏度。
湍流的计算需要选用合适的湍流模型,本研究选用了κ-ω SST模型,该湍流模型是一种用于求解雷诺平均Navier-Stokes方程中涡流黏度的双方程模型。该模型应用于心脏泵的效果较好,因为其可将近壁区的标准低雷诺数κ-ω模型与远场的高雷诺数κ-ω模型相结合。计算过程中,将叶轮定义为旋转区域,将固体壁面定义为无滑移,旋转区域与静止区域的交界面采用滑移网格计算。
将划分完成的网格模型导入仿真软件Fluent中,流体介质为血液,将血液近似看作牛顿流体,血液的密度ρ=1 056 kg/m3, 动力黏度μ=0.003 5 Pa·s。入口设置为速度边界条件,入口速度(换算)范围为1.05~2.09 m/s, 湍流强度为5%。出口边界为自由出流。叶轮表面设置为旋转壁面,其余固定壁面均设置为无滑移边界。为了使流体能够顺利通过流域之间的接触面,各流域接触表面需要设置交互面。选择SIMPLE算法作为压强速度关联算法,离散格式选择二阶迎风格式,最后进行求解计算。
1.3 溶血计算模型
离心式心脏泵流场中会产生很高的非生理性剪切应力,由此导致的溶血问题一直是心脏泵研究人员关注的焦点。传统的溶血预测模型基于库特流剪切装置的体外溶血数据,其认为溶血量与有效剪切应力和暴露时间t呈指数关系,具体关系如下:
$$ H I(\%)=\frac{h b}{H b} \times 100=C \tau_e^\alpha t^\beta $$ (4) 式中, HI表示溶血指数; τe表示有效剪切应力; Hb表示血红蛋白的总浓度; hb表示溶血导致血浆中游离血红蛋白的增加量; C、α、β为经验常数,通过多次实验数据拟合得出。该幂定律模型最早由GIERSIEPEN M等[5]提出,通过实验数据得到常数值C=3.62×10-5, α=2.416, β=0.785。HEUSER G等[6]利用库叶特黏度计进行实验,剪切应力为40~700 Pa, 暴露时间为0.003 4~0.600 0 s, 对数据进行处理后得到常数值C=1.8×10-6, α=1.991, β=0.765。该条件下的参数在既往研究过程中已被多次证明更符合实际流场中情况[7], 本研究采用该组参数值进行计算。剪切应力的表达式为[8]:
$$ \tau_e=\left[\frac{1}{6} \sum\left(\tau_{i i}-\tau_{j j}+\sum \tau_{i j}^2\right]^{\frac{1}{2}}\right. $$ (5) 结合公式(4)与公式(5)计算血泵的溶血指数值,从而衡量血泵的抗溶血性能。
1.4 观察指标
心脏泵使用过程中仍然存在溶血和血栓现象,溶血是指血液中红细胞的细胞膜受到破坏后血红蛋白游离到血清中的现象[9], 血栓是指血小板被激活后沉淀在血液接触面上的现象。由于悬浮过程中液力轴承悬浮间隙较小,该区域血液流速较慢,剪切应力较大,容易出现溶血和血栓现象[10]。本研究主要观察心脏泵的悬浮性能与抗溶血性能,溶血主要受剪切应力和暴露时间的影响,因此需通过计算流体动力学方法对心脏泵的悬浮性能与悬浮轴承间隙处速度、压力等参数进行分析。将改进结构(改进后)与未改进的参照结构(改进前)进行比较,验证改进结构对心脏泵悬浮性能和抗溶血性能的影响。
2. 结果
2.1 心脏泵的水力性能分析
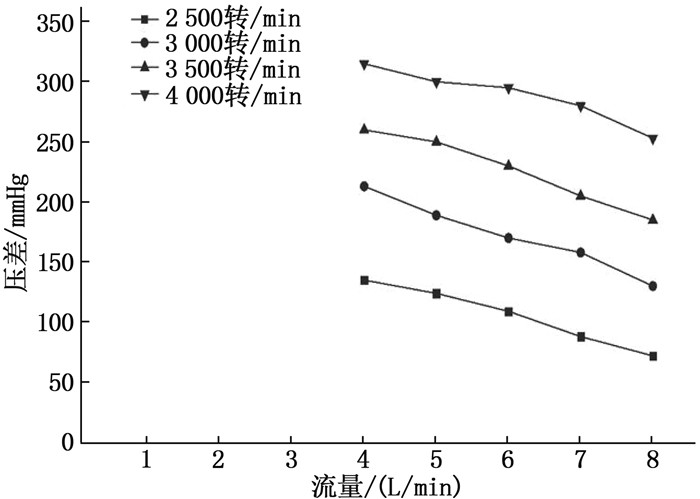
改进后,心脏泵在血液中的流量压差关系见图 3。本研究仅对与心脏泵实际情况接近的4~8 L/min流量进行仿真,仿真结果显示,心脏泵出入口压差值随流量增大而减小,且随叶轮转速提高而增大,与心脏泵在流体中流量压差情况相同,改进后心脏泵的压差值在允许范围内,提示结构改进具有可行性。取转速2 500转/min、流量6 L/min作为心脏泵的标准工况,进行后续仿真分析与心脏泵悬浮性能和抗溶血性能的研究。
2.2 心脏泵的受力与悬浮性能分析
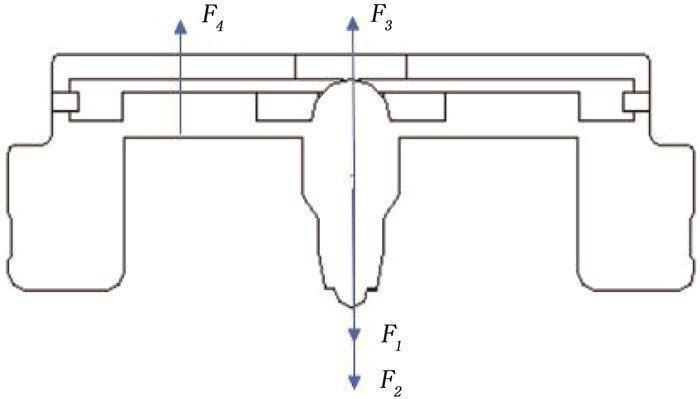
为更好地研究人工心脏泵的支承结构与悬浮性能,本研究对心脏泵受力情况进行分析(因本研究着重于平衡轴向力,故仅对轴向力进行分析)。心脏泵叶轮整体受力分析结果见图 4: F1为叶轮的重力,方向沿轴向竖直向下; F2是在叶轮旋转过程中,由于叶轮和壳体面的血压不均匀且血泵入口处存在血液冲击作用而产生, F2过大将使心脏泵转子撞击泵壳,甚至导致心脏泵失效; F3是由液力轴承产生的悬浮力,上述轴向力F1与F2均不利于叶轮在泵腔中悬浮,故在心脏泵轴向方向设置液力轴承,为转子提供轴向方向的被动悬浮力; F4是由叶轮产生的升力,升力方向向上。
改进结构前后2 500转/min工况时叶轮上下表面压差值见表 1。结果显示,叶轮上下表面的压差值随着流量的增大而减小,改进结构后叶轮底部上下表面的压差值明显增大,轴向方向向上的悬浮力增大。由此提示,改进后的支承结构能够有效减小心脏泵在旋转时所需的悬浮力。
表 1 改进结构前后叶轮上下表面压差值mmHg 时点 流量 5 L/min 6 L/min 7 L/min 改进结构前 8.3 5.5 3.5 改进结构后 21.2 18.5 16.3 2.3 心脏泵的流场与溶血分析
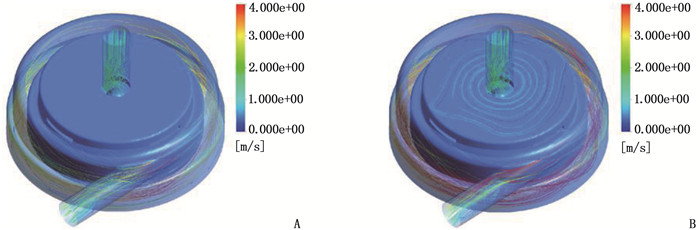
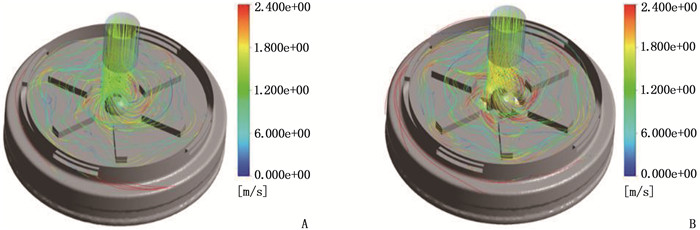
提取心脏泵流场流线图,改进后,叶轮与蜗壳间隙处流体流速提升,血液在心脏泵中暴露时间减少,有利于减小心脏泵叶轮与蜗壳间隙的血液滞留区,心脏泵整体区域没有局部漩涡与流动停滞区,见图 5。提取心脏泵叶片处流线图,改进后,叶轮中心开孔处速度提升,且流体可沿开孔后流道进入叶轮底部,叶片顶端速度相较改进前有所提升,见图 6。由此表明,改进后,血液在心脏泵中流速加快,暴露时间减少,血液滞留区减小。
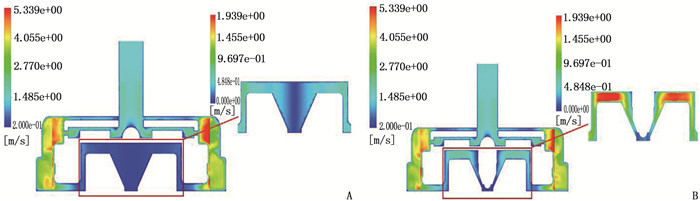
分析改进前后的中心截面速度云图,并对液力轴承悬浮间隙处进行放大,结果显示,速度较低的区域主要集中在轴承底部,此处易产生血液停滞区,需着重关注。相较于改进前,改进后轴承底部速度有所提升,底部区域速度的最高值和平均值均提高,底部区域血液流动加快,停滞区面积减小,可有效改善轴承底部的溶血情况。见图 7。
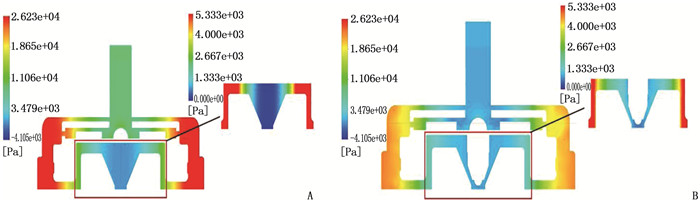
为了进一步验证改进后心脏泵液力轴承悬浮间隙处的抗溶血性能,本研究分析了轴承底部区域压力云图,见图 8。改进后,心脏泵底部区域压力有所减小,压强较高的区域占比明显降低,叶片顶端压力最大值减小,有利于减少心脏泵中血液产生回流与剪切力。改进后底部区域血液所受压力与剪切力减小,进一步验证了改进后心脏泵可有效减少底部区域溶血。
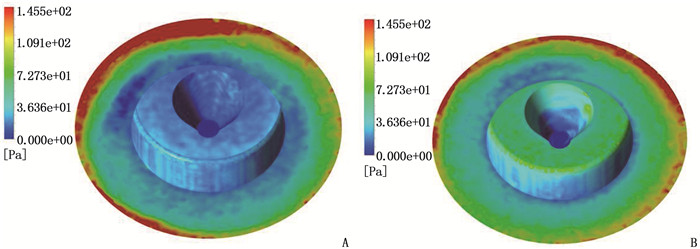
改进前后心脏泵底部剪切应力云图分析结果显示,剪切应力较大的区域主要为底面外围部分,改进结构后底部外围部分的剪切应力大于100 Pa区域相对较小,剪切应力大于130 Pa区域占比降低,而低于130 Pa区域占比较高,见图 9。改进后,底面整体的平均剪切应力降低,表明改进结构可以有效减少心脏泵底部区域溶血现象的发生。
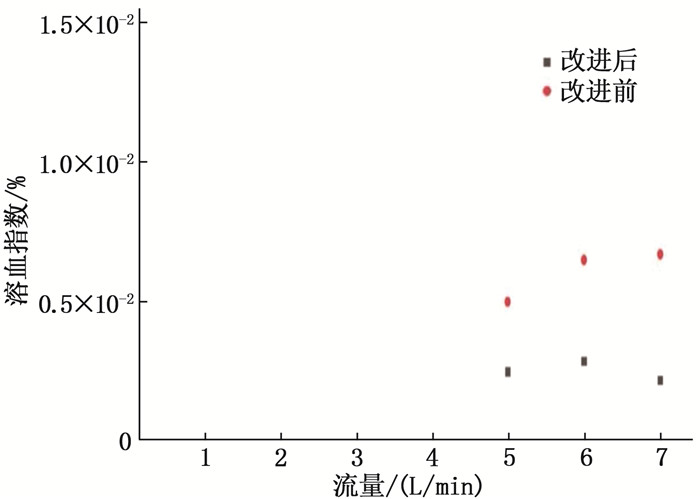
选取入口流量分别为5、6、7 L/min的心脏泵进行观察,比较其改进结构前后的溶血情况,见图 10。仿真结果显示, 2 500转/min的转速下,改进后结构计算得到的溶血指数值低于改进前结构。入口流量分别为5、6、7 L/min的情况下,改进结构后心脏泵的溶血指数相较于改进前降低了12%, 表明改进结构具有降低溶血指数值的效果。
3. 讨论
经过多代的发展后,心脏泵因其优秀的适应性和简单的结构已被广泛应用于心血管疾病治疗领域。WIEGMANN L等[11]研究泵内流场中的间隙、叶片数量和叶轮外壳设计变化的影响发现,低叶片数和半开式叶轮可减小血液停滞区和再循环区的范围。REZAIENIA M A等[12]发现,在给定轴向间隙条件下,随着径向间隙的减小,心脏泵的抗溶血性能提升。GAWLIKOWSKI M等[13]证实,泵壳与叶轮之间的间隙大小对血液创伤程度至关重要。刘泽辉等[14]研究叶片不同参数对剪切力的影响发现,叶片高度越高,叶片顶端间隙越小,则溶血指数值越高。王静月[15]在重力场、流体场等多场耦合的条件下分析叶轮受力情况,并设计了一种结构紧凑的悬浮支承结构。武悦等[16]设计了一种喷射悬浮心脏泵,且发现喷射悬浮方式可在较大间隙下实现转子悬浮。心脏泵发展潜力巨大,但仍存在精度较差,样本数据不足,实际使用过程中可发生溶血、血栓等问题。
计算流体动力学结合溶血模型是目前预测溶血的常用方法[17]。本研究基于计算流体动力学仿真法设计了一种新的心脏泵悬浮支承结构,并结合仿真结果对该支承结构下的离心式心脏泵的悬浮性能和抗溶血性能进行分析与验证。根据成人心脏的生理数据,心脏供血扬程通常为80~120 mmHg, 供血流量为4~10 L/min[18], 心脏泵出入口压差需要满足人体心脏供血扬程,改进后心脏泵在流体中流量压差情况相同,压差值在允许范围内。血细胞撞击速度大于6 m/s时易发生红细胞破损造成溶血[19], 本研究设计优化的心脏泵内血液最大流速低于6 m/s, 故改进结构具有可行性。改进后,在液力轴承悬浮间隙处,流体流速提升,压力减小。当红细胞受到150~1 000 Pa剪切应力时,血红蛋白将进入血液中,引发溶血现象[9], 故剪切应力的大小对溶血结果至关重要。改进后,心脏泵底部区域的剪切应力最大值与高剪切应力区域占比均相对降低,液力轴承悬浮间隙处和底部区域溶血指数降低。本研究仿真结果证明,改进后结构可有效改善心脏泵存在的轴承悬浮间隙过小所致间隙区域血液流速较慢和易产生溶血的问题。此外,改进的悬浮结构也可应用于其他离心式心脏泵,其在增加心脏泵悬浮力与减少悬浮轴承间隙处溶血方面具有实际价值。
-
表 1 改进结构前后叶轮上下表面压差值
mmHg 时点 流量 5 L/min 6 L/min 7 L/min 改进结构前 8.3 5.5 3.5 改进结构后 21.2 18.5 16.3 -
[1] 叶桂萍. 整体护理干预对老年冠心病心脏介入治疗的影响[J]. 中国医药导报, 2008, 5(34): 145-146. doi: 10.3969/j.issn.1673-7210.2008.34.099 [2] 中国心血管健康与疾病报告编写组, 胡盛寿. 中国心血管健康与疾病报告2020概要[J]. 中国循环杂志, 2021, 36(6): 521-545. doi: 10.3969/j.issn.1000-3614.2021.06.001 [3] BENJAMIN E J, MUNTNER P, ALONSO A, et al. Heart disease and stroke statistics-2019 update: a report from the American heart association[J]. Circulation, 2019, 139(10): e56-e528.
[4] 刘英明, 杨晔. 慢性心力衰竭器械治疗进展[J]. 临床心血管病杂志, 2017, 33(10): 1018-1022. doi: 10.13201/j.issn.1001-1439.2017.10.024 [5] GIERSIEPEN M, WURZINGER L J, OPITZ R, et al. Estimation of shear stress-related blood damage in heart valve prostheses: in vitro comparison of 25 aortic valves[J]. Int J Artif Organs, 1990, 13(5): 300-306. doi: 10.1177/039139889001300507
[6] HEUSER G, OPITZ R. A Couette viscometer for short time shearing of blood[J]. Biorheology, 1980, 17(1/2): 17-24.
[7] SONG X, THROCKMORTON A L, WOOD H G, et al. Quantitative evaluation of blood damage in a centrifugal VAD by computational fluid dynamics[J]. Journal of Fluids Engineering, 2004, 126(3): 410-418. doi: 10.1115/1.1758259
[8] BLUDSZUWEIT C. Model for a general mechanical blood damage prediction[J]. Artif Organs, 1995, 19(7): 583-589. doi: 10.1111/j.1525-1594.1995.tb02385.x
[9] BEHBAHANI M, BEHR M, HORMES M, et al. A review of computational fluid dynamics analysis of blood pumps[J]. Eur J Appl Math, 2009, 20: 363-397. doi: 10.1017/S0956792509007839
[10] KOSAKA R, YADA T, NISHIDA M, et al. Geometric optimization of a step bearing for a hydrodynamically levitated centrifugal blood pump for the reduction of hemolysis[J]. Artif Organs, 2013, 37(9): 778-785.
[11] WIEGMANN L, BOËS S, DE ZÉLICOURT D, et al. Blood pump design variations and their influence on hydraulic performance and indicators of hemocompatibility[J]. Ann Biomed Eng, 2018, 46(3): 417-428. doi: 10.1007/s10439-017-1951-0
[12] REZAIENIA M A, PAUL G, AVITAL E, et al. Computational parametric study of the axial and radial clearances in a centrifugal rotary blood pump[J]. Asaio J, 2018, 64(5): 643-650. doi: 10.1097/MAT.0000000000000700
[13] GAWLIKOWSKI M, KURTYKA P, ZALEWSKI J, et al. Methodology for measuring the gap size using a fiber-optic displacement sensor exemplified by a centrifugal blood pump[J]. Photonics Letters of Poland, 2020, 12(2): 46-48. doi: 10.4302/plp.v12i2.1017
[14] 刘泽辉, 张松, 屈一飞. 基于计算流体动力学仿真的离心式人工心脏泵叶片参数优化[J]. 工具技术, 2021, 55(10): 51-57. doi: 10.3969/j.issn.1000-7008.2021.10.010 [15] 王静月. 人工心脏磁液悬浮支承结构设计及性能研究[D]. 哈尔滨: 哈尔滨理工大学, 2020. [16] 武悦, 朱良凡, 罗云. 计算流体力学方法分析一例喷射悬浮血泵的液力、悬浮及溶血特性[J]. 机械工程学报, 2018, 54(20): 52-58. https://www.cnki.com.cn/Article/CJFDTOTAL-JXXB201820006.htm [17] FERZIGER J H. Computational methods for fluid dynamics[M]. Switzerland: Springer, 2020: 239-256.
[18] SONG G, CHUA L P, LIM T M. Numerical study of a bio-centrifugal blood pump with straight impeller blade profiles[J]. Artif Organs, 2010, 34(2): 98-104. doi: 10.1111/j.1525-1594.2009.00756.x
[19] 云忠, 谭建平. 基于血液撞击损伤机理的高速螺旋血泵仿真分析[J]. 中南大学学报: 自然科学版, 2008, 39(1): 135-142. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD200801026.htm -
期刊类型引用(0)
其他类型引用(1)




 下载:
下载:

 苏公网安备 32100302010246号
苏公网安备 32100302010246号